BZOJ

BZOJ 2190


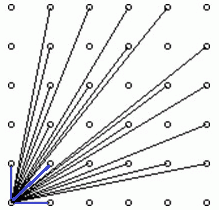
先分析一下题目给的图，发现这张图中有三条永远那么长的线和两个对称的区域，所以答案就是其中一个对称的区域中能看到的人数*2+3


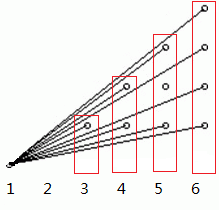
一竖列一竖列来考虑

首先，对于点$(i,j)$，能看到的条件是$gcd(i,j)=1$，否则还能看到$(\frac{i}{gcd(i,j)},\frac{j}{gcd(i,j)})$等点，显然它们共线，矛盾

对于第$i$列，能看到的点数即为$gcd(i,j)=1(j\in[2,i-1])$的数量，就是说在$[2,i-1]$内与$i$互质的数的数量，也就是$\varphi(i-1)$

然后求欧拉函数就好了

先用筛法求素数，然后根据求出的素数利用欧拉函数的性质来求，用到的性质如下：

  • 若x为素数，则$\varphi(x)=x-1$

  • 若$a,b$互质，则$\varphi(a*b)=\varphi(a)*\varphi(b)$

  • 若b为质数且$a\ mod\ b=0$，则$\varphi(a*b)=\varphi(a)*b$

没了，有啥问题看代码吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
program bzoj_2190;
var phi,p:array[1..40000]of longint;
    n,cnt,i,j,ans:longint;
    prime:array[1..40000]of boolean;
begin
  readln(n);
  fillchar(prime,sizeof(prime),true);
  cnt:=0;
  for i:=2 to n do
  begin
    if prime[i] then
    begin
      inc(cnt);
      p[cnt]:=i;
      phi[i]:=i-1;
    end;
    for j:=1 to cnt do
    begin
      if i*p[j]>=n then break;
      prime[i*p[j]]:=false;
      if i mod p[j]=0 then
      begin
        phi[i*p[j]]:=phi[i]*p[j];
        break;
      end else phi[i*p[j]]:=phi[i]*(p[j]-1);
    end;
  end;
  ans:=0;
  for i:=2 to n-1 do inc(ans,phi[i]);
  writeln(ans*2+3);
end.